機械学習アルゴリズムの研究紹介

人工知能（AI）の急速な発展に伴い、機械学習、深層学習といった言葉をよく耳にします。この「学習」とは、いったい何を指すのでしょうか。「学習」とは、望ましい結果が得られるように機械に関するネットワークやパラメータを調整する作業と言えます。もう少し数理的に表現すると、正解データとネットワークからの出力データとの誤差を最小化（最適化）するようにパラメータを調整することです。多くの機械学習手法はデータに対するモデル出力の誤差（損失関数と呼ばれる）を定義し、誤差を最小化するようにパラメータの更新（学習）を行います。 このように、機械学習と最適化はとても密接な関係があります。

機械学習に現れる損失最小化問題は、一般に、以下のように表現できます。 \begin{align*} \text{Minimize } f(x):= \sum_{t\in \mathcal{T}} f_t (x) \text{ subject to } x\in X. \end{align*} ただし、$f_t \colon \mathbb{R}^d \to \mathbb{R}$ $(t\in \mathcal{T}:= \{1,2,\ldots,T\})$ は $t$ 番目の訓練データに関する損失関数、 $X$ $(\subset \mathbb{R}^d)$ は空でない閉凸集合です。

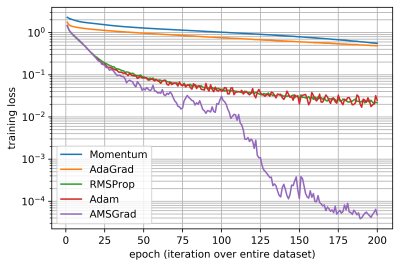
この損失最小化問題手法を解くための機械学習手法として、確率的勾配降下法とそれに基づいた強力な手法がすでに提案されています。 例えば、モメンタム法、AdaGrad、 RMSProp、 Adam や AMSGrad があります。

畳み込み層が20からなる ResNet-20 を用いた画像分類の結果は以下の通りとなります。既存機械学習手法に関する、エポック数¹⁾に対する損失関数 $f$ のグラフです。ここで適用したアルゴリズムは経験的に良いとされている学習率²⁾を利用しています。

ですが、これらのアルゴリズムを利用する際の最も困難な問題は、機械学習を適切に行うための学習率の調整です。例えば、適応学習率最適化アルゴリズムである Adam や AMSGrad の収束解析に依ると、学習率 $\alpha_t = \alpha/\sqrt{t}$ （ただし、$\alpha > 0$） を有する Adam や AMSGrad は \begin{align*} R(T) = \sum_{t\in \mathcal{T}} f_t (x_t) - \underbrace{\sum_{t\in \mathcal{T}} f_t (x^\star)}_{f^\star} \end{align*} で定義されるリグレット（ただし、$(x_t)_{t\in \mathcal{T}}$ は学習アルゴリズムで生成される点列、$x^\star$ は損失最小化問題の解）に対して、 \begin{align*} \frac{R(T)}{T} \leq M \sqrt{\frac{1+ \log T}{T}} \end{align*} を満たします³⁾（ただし、$M$ は定数）が、損失最小化問題を高速に解くための適切な $\alpha$ を事前に設定することは大変難しいです⁴⁾。この問題は、機械学習分野に限らず、一般の最適化アルゴリズムにおいても同様に困難とされています。 加えて、既存の適応学習率最適化アルゴリズムは（$R(T)/T \approx 0$ の意味でリグレット最小化を保証しますが）損失最小化問題を解くことが保証されていません。

• H. Iiduka: Appropriate Learning Rates of Adaptive Learning Rate Optimization Algorithms for Training Deep Neural Networks, preprint.

適切な学習率の設定を考慮しつつ、損失最小化問題を解くことを保証する適応学習率最適化アルゴリズムについて提案しています。
$0$に収束するような減少学習率 （例えば、$\alpha_t = \alpha/\sqrt{t}$） を有する既存の適応学習率最適化アルゴリズム Adam や AMSGrad の収束解析とは異なり、定数学習率を有する適応学習率最適化アルゴリズムの収束解析を与えています。具体的には、以下の通りです。 $(x_n)_{n\in\mathbb{N}}$は適応学習率最適化アルゴリズムで生成される点列とし、$\alpha, \beta$ は定数学習率⁵⁾とします。このとき、ある定数 $M_i$ ($i=1,2$) が存在して、 \begin{align*} \limsup_{n \to + \infty} \mathbb{E}\left[f (x_n) - f^\star \right] \leq M_1 \alpha + M_2 \beta. \end{align*} $M_i$ ($i=1,2$) はアルゴリズムを実行させる前に計算可能な定数であるため、この不等式の右辺が十分小さくなるように定数学習率 $\alpha, \beta$ を適切に設定できます。少し大まかに言うと、小さな定数学習率を有する適応学習率最適化アルゴリズムが損失最小化問題の解を近似できる、となります。
これまでの減少学習率に対する適応学習率最適化アルゴリズムの収束解析では、リグレット最小化のみが保証されており、損失最小化問題を解くことまでは保証されていませんでした。 この論文では、減少学習率を有する適応学習率最適化アルゴリズムで生成される点列の任意の集積点が損失最小化問題の解集合に属することを数学的に証明しています。詳細については、こちらをご参照下さい。（説明終わり）

• Y. Kobayashi and H. Iiduka: Conjugate-gradient-based Adam for Stochastic Optimization and Its Application to Deep Learning, preprint.

既存の適応学習率最適化アルゴリズムと比べて高速に深層ニューラルネットワークを訓練可能なアルゴリズム CoBA を提案しています。主なアイデアは、既存の適応学習率最適化アルゴリズム Adam、AMSGrad で利用している確率勾配方向 $d_t = - g_t$ を共役勾配方向 \begin{align*} d_t = - g_t + \gamma_t d_{t-1} \end{align*} に修正した点です。非線形共役勾配法は高速に最適化問題を解くための有用な手法の一つであるため、非線形共役勾配法と既存の適応学習率最適化アルゴリズムを合わせた CoBA の提案は自然であると思います。 本論文では、 CoBA がリグレット最小化に関して、AMSGrad と同等の性能を有することを数学的に証明しています。 更に、テキスト分類や画像分類に対する モメンタム法、AdaGrad、 RMSProp、 Adam、AMSGrad といった既存アルゴリズムと CoBA の性能比較を行い、CoBA が既存アルゴリズムと比べて高速に損失関数 $f$ を最小化し、かつ、高い分類精度を得ることを示しています。 詳細については、こちらをご参照下さい。（説明終わり）

• K. Hishinuma and H. Iiduka: Incremental and Parallel Machine Learning Algorithms With Automated Learning Rate Adjustments, Frontiers in Robotics and AI: Resolution of Limitations of Deep Learning to Develop New AI Paradigms, Vol. 6, Article 77, 2019.

直線探索法に基づいた適切な学習率を利用できるアルゴリズムについて提案しています。 多層ニューラルネットワークなどといった深層学習においては、そのネットワークの規模に応じて扱う問題の次元が大きくなります。 そのような問題を既存手法で効率的に解くためには、学習する問題やネットワークに対して最適な学習率を事前にアルゴリズムに与える必要があります。 しかしながら提案手法では、実行時に自動的に適切な学習率を直線探索法により探索するので、学習率の事前の精密な調整を必要とせずに用いることができます。 本論文では、直線探索法を取り入れた増分劣勾配法や並列型劣勾配法が制約付き非平滑凸最適化問題の解へ収束する点列を生成することを数学的に証明するとともに、これらの手法を多層ニューラルネットワークの学習に適用して、深層学習への活用可能性について議論しています。（説明終わり）

グラフやテキストなどのデータを双曲空間の Poincaré 円板モデル へ埋め込む Poincaré 埋め込みを利用することで、⾼次元の Euclid 空間でも実現できなかった高精度埋め込みを実現できる場合があります。Poincaré 円板モデル の図にもあるように、縁に進むほど密になる性質があるため、Poincaré 円板モデルは木構造データを埋め込むのに適していると言えます。 Poincaré 円板は Riemann 多様体構造を持つため、 以下のような Riemann 多様体上の損失最小化問題を解くことを考えます。 \begin{align*} \text{Minimize } f(x):= \sum_{t\in \mathcal{T}} f_t (x) \text{ subject to } x\in X. \end{align*} ただし、$M_i$ は測地的完備 Riemann 多様体、$M = M_1 \times \cdots \times M_N$、$f_t \colon M \to \mathbb{R}$ $(t\in \mathcal{T}:= \{1,2,\ldots,T\})$ は $t$ 番目の訓練データに関する損失関数、$X_i \subset M_i$ は空でない測地的凸集合、 $X= X_1 \times \cdots \times X_N$ です。
この損失最小化問題手法を解くための機械学習手法として、Euclid 空間上の確率的勾配降下法を拡張したRiemann 確率的勾配降下法 (RSGD) がすでに提案されています。 そこで、 Adam や AMSGrad といった Euclid 空間上の適応学習率最適化アルゴリズムを一般の Riemann 多様体上に拡張することは、Riemann 多様体上の損失最小化問題を高速に解くためには大変自然な発想であると思います。 しかしながら、Euclid 空間上の適応学習率最適化アルゴリズムの多様体上への拡張は、一般の多様体上に共通する座標系が存在しないことが原因となり、容易ではないと考えられます。 そこで、積多様体の成分を Euclid 空間における座標成分のようにみなして AMSGrad を Riemann 積多様体上に拡張した手法 Riemannian AMSGrad (RAMSGrad) が 2019 年に G. Bécigneul と O.-E. Ganea によって提案されました。 しかしながら、Euclid 空間上の機械学習アルゴリズム内でも示したように、 減少学習率 $\alpha_t = \alpha/\sqrt{t}$ を有するRAMSGrad は \begin{align*} R(T) = \sum_{t\in \mathcal{T}} f_t (x_t) - f^\star \end{align*} で定義されるリグレット（ただし、$(x_t)_{t\in \mathcal{T}}$ は学習アルゴリズムで生成される点列、$f^\star$ は損失最小化問題の最適値）に対して、 \begin{align*} \frac{R(T)}{T} \leq M \sqrt{\frac{1+ \log T}{T}} \end{align*} を満たします （ただし、$M$ は定数） が、損失最小化問題を解くことが保証されていません。また、適切な学習率設定と実用の観点から、定数学習率での収束解析は必要です⁶⁾。

• H. Sakai and H. Iiduka: Riemannian Adaptive Optimization Algorithm and Its Application to Natural Language Processing, preprint.

適切な学習率の設定を考慮しつつ、損失最小化問題を解くことを保証する適応学習率最適化アルゴリズムについて提案しています。
$0$に収束するような減少学習率 （例えば、$\alpha_t = \alpha/\sqrt{t}$） を有する既存の適応学習率最適化アルゴリズム RAMSGrad の収束解析とは異なり、定数学習率を有する適応学習率最適化アルゴリズムの収束解析を与えています。具体的には、以下の通りです。 $(x_n)_{n\in\mathbb{N}}$は適応学習率最適化アルゴリズムで生成される点列とし、$\alpha, \beta$ は定数学習率とします。このとき、ある定数 $C_i$ ($i=1,2$) が存在して、 \begin{align*} \mathbb{E} \left[\frac{1}{n} \sum_{k=1}^n f(x_k) - f^\star \right] \leq \mathcal{O}\left(\frac{1}{n}\right) + C_1 \alpha + C_2 \beta. \end{align*} $C_i$ ($i=1,2$) はアルゴリズムを実行させる前に計算可能な定数であるため、この不等式の右辺が十分小さくなるように定数学習率 $\alpha, \beta$ を適切に設定できます。大まかに言うと、小さな定数学習率を有する適応学習率最適化アルゴリズムが損失最小化問題の解を近似できる、となります。
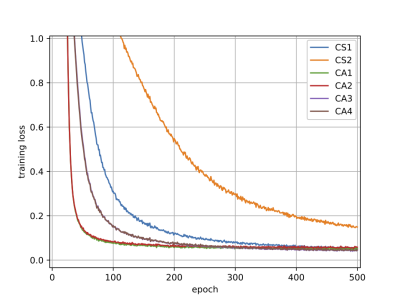
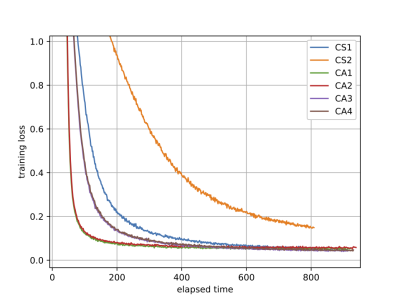
これまでの減少学習率に対する適応学習率最適化アルゴリズムの収束解析では、リグレット最小化のみが保証されており、損失最小化問題を解くことまでは保証されていませんでした。 この論文では、減少学習率を有する適応学習率最適化アルゴリズムが損失最小化問題を解くことができます。 WordNet の単語全体 (82,115単語) を 5 次元 Poincaré 円板へ埋め込んだ際の結果は以下のようになります。 定数学習率を有する RSGD (CS1, CS2) と提案手法 (CA1–CA4) に関する、実行時間及びエポック数に対する損失関数 $f$ のグラフです。 得られた収束解析に基づいて設定した定数学習率を有する提案手法 (CA2, 定数学習率を有する RAMSGrad と殆ど同様) が良い性能を有することを示しています。

詳細については、こちらをご参照下さい。（説明終わり）

アンサンブル学習法とは、複数の学習器を訓練し、それらを組み合わせて将来を予測することができる最先端の学習法のことです。これまでに、ノイズに対する頑強なアンサンブル構築のための疎性 (sparsity) と安定したアンサンブル構築のための多様性 (diversity) とを考慮したアンサンブル法を提案しています。
ここで考察される損失最小化問題は、以下のように定義されます。 \begin{align*} \text{Minimize } f(x) := \sum_{t\in\mathcal{T}} f_t (x) \text{ subject to } x \in X = \mathbb{R}_+^d \cap \underbrace{\left\{ x \in \mathbb{R}^d \colon \|x\|_1 \leq t_1 \right\}}_{C_{\mathrm{s}}} \cap \underbrace{\left\{ x \in \mathbb{R}^d \colon f_{\mathrm{div}}(x) \geq t_2 \right\}}_{C_{\mathrm{d}}}. \end{align*} ただし、$\mathbb{R}_+^d = \{ (x_i)_{i=1}^d \in \mathbb{R}^d \colon x_i \geq 0 \text{ } (i=1,2,\ldots,d)\}$、$\|\cdot\|_1$ は $\ell_1$-ノルム⁷⁾、$f_{\mathrm{div}} \colon \mathbb{R}^d \to \mathbb{R}$ は多様性に関する評価関数、$t_1$ は疎性制御パラメータ、$t_2$ は多様性制御パラメータを表します。 この損失最小化問題を解くために、確率的勾配降下法を適用すると、以下のようになります。 \begin{align*} x_{n+1} = P_X (x_n - \alpha_n \mathsf{G}(x_n,t_n)) \quad (n \in \mathbb{N}). \end{align*} ただし、$\alpha_n >0$ は学習率、$\mathsf{G}(x,t_n) \in \partial f_{t_n}(x)$ は確率勾配、$P_X$ は制約集合 $X$ への距離射影⁸⁾です。

$X = \mathbb{R}_+^d \cap C_{\mathrm{s}} \cap C_{\mathrm{d}}$ という定義から、$P_X$ の計算は容易ではありません。 そのため、残念ながら確率的勾配降下法はアンサンブル学習に関しては有用な手法とは言えません。ここで、不動点近似法を利用します。具体的には、 $\mathbb{R}_+^d$ への距離射影を $P_+$、$C_{\mathrm{s}}$ 及び $C_{\mathrm{d}}$ に関する射影⁹⁾をそれぞれ $P_{\mathrm{s}}, P_{\mathrm{d}}$ としたとき、それらの平均写像 \begin{align*} Q = w_1 P_+ + w_2 P_{\mathrm{s}} + w_3 P_{\mathrm{d}} \end{align*} が定義できます。$P_+, P_{\mathrm{s}}, P_{\mathrm{d}}$ は計算可能なので、写像 $Q$ も容易に計算可能です。更に、不動点近似法の理論により、 $Q$ は準非拡大写像となり、 $\mathrm{Fix}(Q) = X$ を示すことができます。この事実により、$Q$ を取り入れたアルゴリズムで生成される点列は $Q$ の不動点、すなわち、$X$ の点を見つけることが期待できそうです。

• H. Iiduka: Stochastic Fixed Point Optimization Algorithm for Classifier Ensemble, IEEE Transactions on Cybernetics (accepted) PDF

この論文では、以下で定義される確率的不動点最適化アルゴリズムを提案しています。 \begin{align*} x_{n+1} = Q(x_n) - \alpha_n \mathsf{G}(Q(x_n), t_n)\quad (n \in \mathbb{N}). \end{align*} 定数学習率 $\alpha$ に対しては、ある定数 $K_i$ $(i=1,2)$ が存在して、以下が成り立ちます。 \begin{align*} \liminf_{n\to + \infty} \mathbb{E} \left[\| x_n - Q(x_n) \|^2 \right] \leq K_1 \alpha, \text{ } \liminf_{n \to + \infty} \mathbb{E} \left[ f(x_n) - f^\star \right] \leq K_2 \sqrt{\alpha}. \end{align*} これらの不等式は、十分小さい定数学習率を有する確率的不動点最適化アルゴリズムは損失最小化問題の解を近似できることを示しています。 また、減少学習率及び直線探索法で計算された学習率を有する確率的不動点最適化アルゴリズムは損失最小化問題の解に収束することを数学的に証明しています。 詳細については、こちらをご参照下さい。（説明終わり）

• H. Iiduka: Stochastic Approximation Method Using Diagonal Positive-Definite Matrices for Convex Optimization with Fixed Point Constraints, submitted.