機械学習研究

人工知能（AI）の急速な発展に伴い、機械学習、深層学習といった言葉をよく耳にします。この「学習」とは、いったい何を指すのでしょうか。「学習」とは、望ましい結果が得られるように機械に関するネットワークやパラメータを調整する作業といえます。もう少し数理的に表現すると、正解データとネットワークからの出力データとの誤差を最小化（最適化）するようにパラメータを調整することです。多くの機械学習手法はデータに対するモデル出力の誤差（損失関数と呼ばれる）を定義し、誤差を最小化するようにパラメータの更新（学習）を行います。 このように、機械学習と最適化はとても密接な関係があります。

深層ニューラルネットワークに現れる損失最小化問題は、一般に、以下のように表現できます。 \begin{align*} \text{Minimize } f(x):= \frac{1}{n} \sum_{i=1}^n f_i (x) \text{ subject to } x\in X. \end{align*} ただし、$f_i \colon \mathbb{R}^d \to \mathbb{R}$ $(i\in \{1,2,\ldots,n\})$ は $i$ 番目の訓練データに関する損失関数、 $X$ $(\subset \mathbb{R}^d)$ は空でない閉凸集合です。

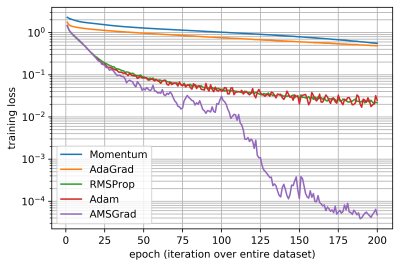
この損失最小化問題手法を解くための深層学習手法（ここではオプティマイザーと呼ぶことにします）として、確率的勾配降下法 (SGD)とそれに基づいた強力な手法がすでに提案されています。 例えば、モーメンタム法、Adaptive Gradient (AdaGrad)、 RMSProp (Root Mean Square Propagation)、 Adaptive Moment Estimation (Adam) や Adaptive Mean Square Gradient (AMSGrad) があります。

CIFAR-10データセットを用いたニューラルネットワーク ResNet-20 の訓練結果は以下の通りとなります。オプティマイザーに関する、エポック数¹⁾に対する損失関数 $f$ のグラフです。ここで適用したオプティマイザーは経験的に良いとされている学習率²⁾を利用しています。

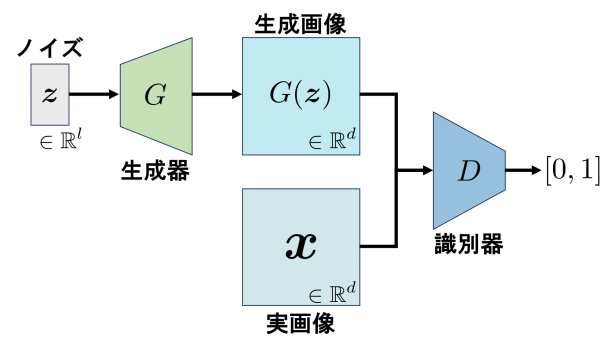
敵対的生成ネットワーク(GAN:Generative Adversarial Networks)の目的関数は、次のように表現できます。

\begin{align*} \min_G \max_D V(D,G):= \mathbb{E}_\boldsymbol{x} [\log D(\boldsymbol{x})] + \mathbb{E}_\boldsymbol{z} [\log (1-D(G(\boldsymbol{z})))]. \end{align*}

ただし、$G:\mathbb{R}^l \to \mathbb{R}^d \ (\boldsymbol{z} \mapsto G(\boldsymbol{z}))$は生成器で、 $D:\mathbb{R}^d \to \mathbb{R} \ (\boldsymbol{x} \ $or$ \ G(\boldsymbol{z})\mapsto [0,1])$は識別器です。
さらに、$\boldsymbol{x} \in \mathbb{R}^d$ は実画像、$\boldsymbol{z} \in \mathbb{R}^l$ はノイズで、 $G(\boldsymbol{z}) \in \mathbb{R}^d$は生成画像です。 実画像の次元$d$は、データセットによって決まっています。例えば、MNISTデータセットならば$d= 28 \times 28 \times 1$となり、CIFAR10データセットならば$d=64 \times 64 \times 3$となります。生成画像の次元は、実画像の次元と等しくなるように生成器が設計されています。ノイズの次元$l$は100や128などと設定されることが多いです。

生成器はノイズ、または潜在変数と呼ばれる$\boldsymbol{z} \in \mathbb{R}^l$を入力とし、生成画像$G(\boldsymbol{z}) \in \mathbb{R}^d$を出力します。
識別器は、実画像$\boldsymbol{x} \in \mathbb{R}^d$または生成画像$G(\boldsymbol{z}) \in \mathbb{R}^d$を入力とし、入力された画像が実画像である確率$[0,1]$を出力します。

生成器は、識別器に見破られない生成画像を作ることを目指すので、$D(\boldsymbol{x})=0, D(G(\boldsymbol{z}))=1$となるように振る舞います。
識別器は、実画像と生成画像を完全に識別することを目指すので、$D(\boldsymbol{x})=1, D(G(\boldsymbol{z}))=0$となるように振る舞います。
すなわち、生成器は$L_G=V$を最小にするように行動し、識別器は$L_D=-V$を最小にするように行動します。
具体的には、生成器と識別器はAdamなどの最適化手法を使って、自身の目的関数が最小になるようなパラメータを探索します。 これを踏まえると、GANの学習は、生成器と識別器をプレイヤーとするナッシュ均衡問題の局所的ナッシュ均衡を見つけようとすることであると言えます。

このように、GANは他の深層生成モデルと比べて高品質な画像を生成することができますが、その学習は非常に不安定であることが知られています。
より早く、より安定した学習で、より高品質な画像を生成するために、たくさんのGANが提案されています。

生成器のニューラルネットワークのパラメータを$\boldsymbol{\theta}$、識別器のニューラルネットワークのパラメータを$\boldsymbol{w}$とします。それぞれの目的関数を最小にすることを目指すので、 \begin{align} \nabla_\boldsymbol{\theta} L_G(\boldsymbol{\theta}_n, \boldsymbol{w}_n)=\boldsymbol{0}, \nabla_\boldsymbol{w} L_D(\boldsymbol{\theta}_n, \boldsymbol{w}_n)=\boldsymbol{0} \end{align} を満たすような最適解$(\boldsymbol{\theta}^\star, \boldsymbol{w}^\star)$を探します。上の等式は、 \begin{align} \forall \boldsymbol{\theta} \in \mathbb{R}^\Theta, \forall \boldsymbol{w} \in \mathbb{R}^W: \langle \boldsymbol{\theta}_n - \boldsymbol{\theta}, \nabla_{\boldsymbol{\theta}} L_G (\boldsymbol{\theta}_n, \boldsymbol{w}_n) \rangle \leq 0 \text{, } \langle \boldsymbol{w}_n - \boldsymbol{w}, \nabla_{\boldsymbol{w}} L_D (\boldsymbol{\theta}_n, \boldsymbol{w}_n) \rangle \leq 0 \end{align} と等価なので、この不等式を満たすような最適解$(\boldsymbol{\theta}^\star, \boldsymbol{w}^\star)$を探しましょう。 上の不等式の左辺について、それぞれ次の不等式が成り立ちます。 \begin{align} &\frac{1}{N} \sum_{n=1}^{N} \mathbb{E} \left[ \langle \boldsymbol{\theta}_n - \boldsymbol{\theta}, \nabla_{\boldsymbol{\theta}} L_G (\boldsymbol{\theta}_n, \boldsymbol{w}_n) \rangle \right] \leq \underbrace{\frac{\Theta \mathrm{Dist}(\boldsymbol{\theta}) H^G}{2 \alpha^G \tilde{\beta_1^G}}}_{A_G} \frac{1}{N} + \underbrace{\frac{\sigma_G^2 \alpha^G}{2 \tilde{\beta_1^G} \tilde{\gamma}^{G^2} h_{0,*}^G}}_{B_G} \frac{1}{b} + \underbrace{\frac{M_G^2 \alpha^G}{2 \tilde{\beta_1^G} \tilde{\gamma}^{G^2} h_{0,*}^G} + \frac{\beta_1^G}{\tilde{\beta_1^G}} \sqrt{\Theta \mathrm{Dist}(\boldsymbol{\theta}) ( \sigma_G^2 + M_G^2 )}}_{C_G}, \\ &\frac{1}{N} \sum_{n=1}^{N} \mathbb{E} \left[ \langle \boldsymbol{w}_n - \boldsymbol{w}, \nabla_{\boldsymbol{w}} L_G (\boldsymbol{\theta}_n, \boldsymbol{w}_n) \rangle \right] \leq \underbrace{\frac{W \mathrm{Dist}(\boldsymbol{w}) H^D}{2 \alpha^D \tilde{\beta_1^D}}}_{A_D} \frac{1}{N} + \underbrace{\frac{\sigma_G^2 \alpha^D}{2 \tilde{\beta_1^D} \tilde{\gamma}^{D^2} h_{0,*}^D}}_{B_D} \frac{1}{b} + \underbrace{\frac{M_D^2 \alpha^D}{2 \tilde{\beta_1^D} \tilde{\gamma}^{D^2} h_{0,*}^D} + \frac{\beta_1^D}{\tilde{\beta_1^D}} \sqrt{W \mathrm{Dist}(\boldsymbol{w}) ( \sigma_D^2 + M_D^2 )}}_{C_D} \end{align} ただし、$\alpha^G, \alpha^D$はoptimizerの学習率で、Nはステップ数、bはバッチサイズです。その他の定義については論文を参照してください。このことから、ステップ数$N$とバッチサイズ$b$を大きく、学習率$\alpha^G, \alpha^D$は小さくすれば、それぞれの右辺は0に近くなり、局所的ナッシュ均衡を近似できることがわかります。

局所的ナッシュ均衡を近似できる理想的なステップ数$N$、バッチサイズ$b$、学習率$\alpha^G, \alpha^D$などのパラメータを設定できたとします。このとき、$\epsilon_G, \epsilon_D > 0$を十分小さい正数だとすると、 \begin{align} \frac{A_G}{N_G}+\frac{B_G}{b}+C_G=\epsilon_G^2, \text{ } \frac{A_D}{N_D}+\frac{B_D}{b}+C_D=\epsilon_D^2 \end{align} すなわち、 \begin{align} N_G(b)=\frac{A_G b}{(\epsilon_G^2 -C_G)b -B_G}, \text{ } N_D(b)=\frac{A_D b}{(\epsilon_D^2 -C_D)b -B_D} \end{align} が成り立ちます。ただし、生成器のステップ数を$N_G$、識別器のステップ数を$N_D$とし、それぞれをバッチサイズ$b$の関数だと捉えています。

クリティカルバッチサイズとは、学習の計算量を最小にするバッチサイズのことです。 ニューラルネットワークの訓練には、クリティカルバッチサイズが存在することが先行研究によって明らかになっています。 そこで、GANの訓練にもクリティカルバッチサイズが存在するかどうかを考えてみましょう。

Naoki Sato, Hideaki Iiduka: Existence and Estimation of Critical Batch Size for Training Generative Adversarial Networks with Two Time-Scale Update Rule, Proceedings of The 40th International Conference on Machine Learning, PMLR 202: ??–?? (2023)

Hiroki Naganuma, Hideaki Iiduka: Conjugate Gradient Method for Generative Adversarial Networks, Proceedings of The 26th International Conference on Artificial Intelligence and Statistics, PMLR 206: 4381–4408 (2023)